Buon PiGreco day. il problema della quadratura del cerchio, ecco perchè è impossibile
Definire la più famosa delle costanti matematiche della storia dell’umanità è qualcosa che ancora oggi risulta un problema di difficile soluzione. Lo studio del rapporto tra circonferenza e diametro del cerchio accompagna la storia dell’umanità fin dall’invenzione della ruota. Intrappolare quel numero in una serie finita di cifre è una impresa che quasi tutti i matematici. E quando nel 1761 il matematico Johan Lambert dimostrò che esso è irrazionale scattò la vera e propria sfida al calcolo del più alto numero di cifre decimali per renderlo quanto più preciso è possibile. La dimostrazione di Lambert segna una svolta perchè dimostra in pratica che il nostro numero non può essere intrappolato nel rapporto tra due numeri, uno a numeratore e uno a denominatore. Di fatto non può essere “razionalizzato”.
Eulero fu uno dei matematici che, partendo da tale considerazione, inizia a definire un calcolo più o meno automatico del Pi-greco:il prodotto infinito..
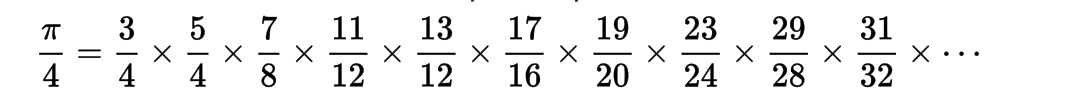
Essa, però, ha una lenta convergenza, nel senso che occorre portare avanti una serie molto lunga di di valori per raggiungere una certa precisione. Qui si comincia a scorgere un sorprendente legame tra Pi-greco e i numeri primi. A numeratore notiamo, infatti, solo numeri primi mentre a denominatore alternativamente il numero precedente o successivo al numeratore. C’è da considerare che il fattore che viene generato di volta in volta converge a 1 proprio per l’assottigliarsi della differenza tra numeratore e denominatore. Un altro metodo sempre utilizzato da Eulero era basato sulla serie armonica:

Essa forse risulta più elegante ma anche questa converge molto lentamente. In ogni caso la grande considerazione che è possibile fare è la seguente:
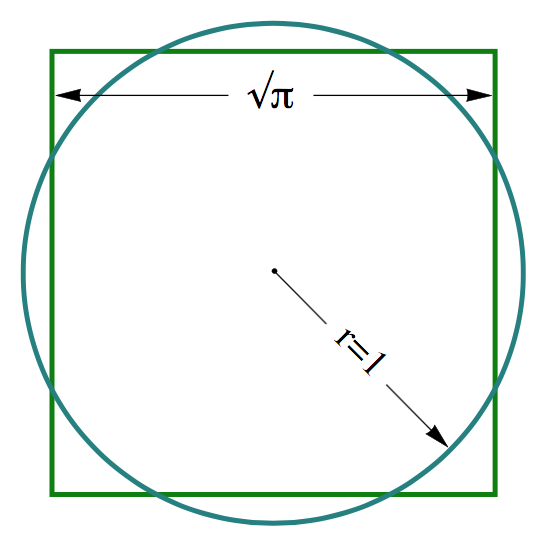
Il numero Pi-Greco è irrazionale ed è anche trascendente ovvero non ci sono polinomi di cui esso è radice. Ciò vuol dire che non lo si può intrappolare in nessuna sequenza numerica finita. Non essendoci polinomi di cui Pi-Greco è radice si dimostra anche che non è possibile creare un poligono regolare o un quadrato la cui area sia equivalente a quella di un cerchio. Infatti, se avessimo una circonferenza di raggio 1, essa avrebbe area PI-Greco e se volessimo costruire un quadrato equivalente dovremmo individuare con precisione assoluta il valore di PI-Greco, anzi, la sua radice quadrata
Ma perchè individuare con la massima precisione il valore di questa costante ha affascinato i matematici di tutte le epoche? Già i Babilonesi si posero questo problema e successivamente gli egizi: π = (16⁄9)2 fu il valore che per la prima volta si avvicinava al 3,14: 3,16. Siamo al XX secolo A.C. Fu Archimede il primo a tentare un calcolo basato sulla geometria attraverso il metodo della esaustione che consisteva nel cercare di intrappolare la circonferenza tra un poligono iscritto e uno circoscritto. Usando poligoni di 96 lati calcolò il valore di Pi-Greco a 3,14163.
Da quel coda quel periodo parte una straordinaria corsa al calcolo del massimo numero di cifre decimali cheti fa sempre più interessanti nell’età contemporanea a partire dall’800, una volta appurato che il nostro numero è irrazionale quindi ha un numero infinito di cifre decimali. Occorre definirne il massimo numero possibile per definire la precisione.
Il calcolo del PI-Greco preciso è stato anche una sfida per dimostrare la potenza di calcolo dei calcolatori elettronici sin dalla loro prima apparizione. L’ENIAC, il primo calcolatore elettronico, nel 1949 calcola 2037 cifre in 70 ore di elaborazione.
Nel 1989 i fratelli Chudnovsky elaborano un algoritmo per il calcolo delle cifre decimali e raggiungono circa un miliardo di cifre decimali su un super calcolatore IBM.
Da allora molti utilizzano quest’ultimo algoritmo. E’ solo una questione di potenza di calcolo. Nel 2010 viene raggiunta la cifra numero 5.000.000.000.000, ovvero 5 trilioni di cifre. A novembre 2016 si arriva ad oltre 22,6 trilioni di cifre decimali. Per raggiungere questo risultato viene utilizzato un calcolatore performante con 4 processori Intel Xeon per un totale di 72 core, 1,25 Terabyte di memoria RAM e ben 20 Hard disk da 6 terabyte ciascuno per la conservazione dei dati. Il calcolo impiega oltre 3 mesi, 105 giorni per l’esattezza.
Ecco un link agli ultimi risultati:
La quadratura del cerchio non verrà mai raggiunta ma la sfida matematica è sempre aperta!!!
Di seguito vi fornisco le prime 1000 cifre decimali di questo numero favoloso:
3,
1415926535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164 0628620899 8628034825 3421170679 8214808651 3282306647 0938446095 5058223172 5359408128 4811174502 8410270193 8521105559 6446229489 5493038196 4428810975 6659334461 2847564823 3786783165 2712019091 4564856692 3460348610 4543266482 1339360726 0249141273 7245870066 0631558817 4881520920 9628292540 9171536436 7892590360 0113305305 4882046652 1384146951 9415116094 3305727036 5759591953 0921861173 8193261179 3105118548 0744623799 6274956735 1885752724 8912279381 8301194912 9833673362 4406566430 8602139494 6395224737 1907021798 6094370277 0539217176 2931767523 8467481846 7669405132 0005681271 4526356082 7785771342 7577896091 7363717872 1468440901 2249534301 4654958537 1050792279 6892589235 4201995611 2129021960 8640344181 5981362977 4771309960 5187072113 4999999837 2978049951 0597317328 1609631859 5024459455 3469083026 4252230825 3344685035 2619311881 7101000313 7838752886 5875332083 8142061717 7669147303 5982534904 2875546873 1159562863 8823537875 9375195778 1857780532 1712268066 1300192787 6611195909 2164201989 3809525720 1065485863 2788659361 5338182796 8230301952 0353018529 6899577362 2599413891 2497217752 8347913151 5574857242 4541506959 5082953311 6861727855


